Is Your Model Really A Good Math Reasoner? Evaluating Mathematical Reasoning with Checklist

Zihao Zhou12*  Shudong Liu3*  Maizhen Ning12  Wei Liu4 
Jindong Wang5  Derek F. Wong3  Xiaowei Huang2  Qiufeng Wang1  Kaizhu Huang6 
1Xi’an Jiaotong-liverpool University  2University of Liverpool  3University of Macau 
4Hong Kong University of Science and Technology  5Microsoft Research Asia 
6Duke Kunshan University  *Equal Contribution
zihao.zhou@liverpool.ac.uk  nlp2ct.shudong@gmail.com 
Paper

🤗

 Dataset Code

🏆

 Results

Overview of MATHCHECK design. The horizontal axis examines the task generalization of four math tasks while the vertical axis examines the reasoning robustness through four problem varieties. All data are generated from seed data, which is also from mainstream benchmark paradigm.

Introduction

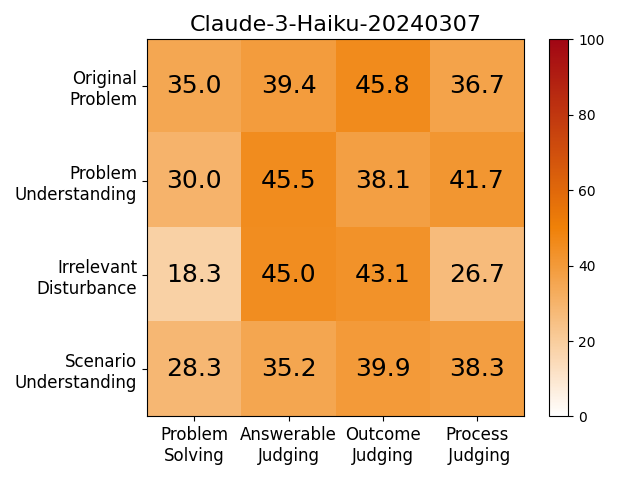
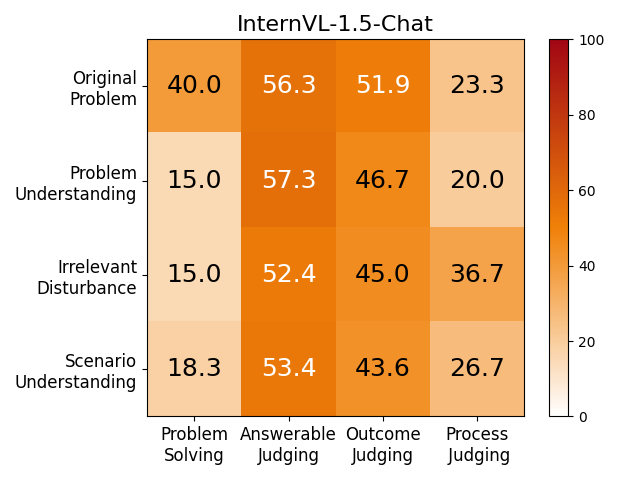
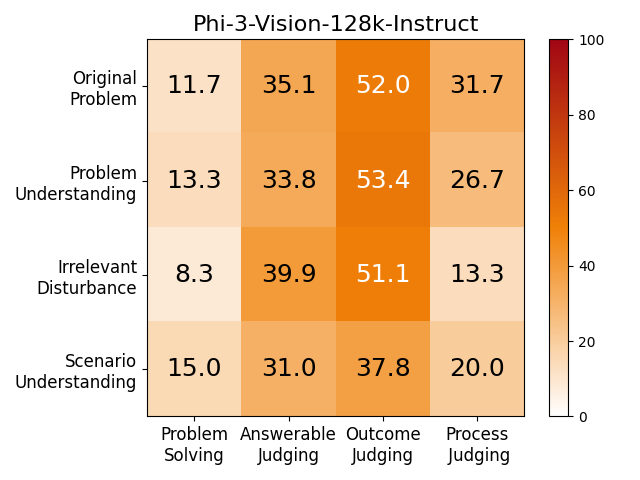
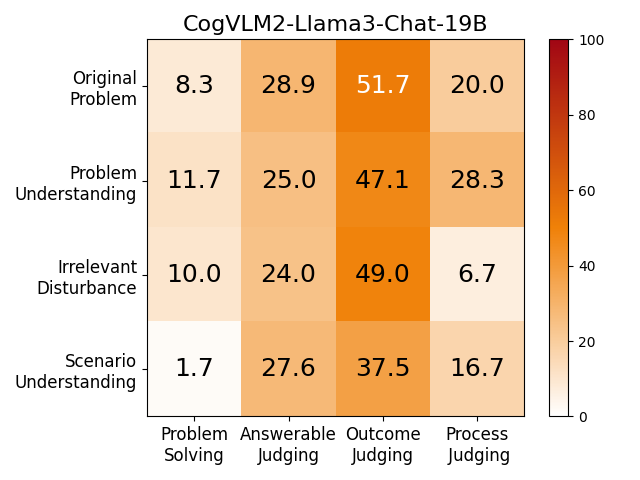
Exceptional mathematical reasoning ability is one of the key features that demonstrate the power of large language models (LLMs). How to comprehensively define and evaluate the mathematical abilities of LLMs, and even reflect the user experience in real-world scenarios, has emerged as a critical issue. Current benchmarks predominantly concentrate on problem-solving capabilities, which presents a substantial risk of model overfitting and fails to accurately represent genuine mathematical reasoning abilities. In this paper, we argue that if a model really understands a problem, it should be robustly and readily applied across a diverse array of tasks.
Motivated by this, we introduce MATHCHECK, a well-designed checklist for testing task generalization and reasoning robustness, as well as an automatic tool to generate checklists efficiently. MATHCHECK includes multiple mathematical reasoning tasks and robustness test types to facilitate a comprehensive evaluation of both mathematical reasoning ability and behavior testing. Utilizing MATHCHECK, we develop MATHCHECK-GSM and MATHCHECK-GEO to assess mathematical textual reasoning and multi-modal reasoning capabilities, respectively, serving as upgraded versions of benchmarks including GSM8k, GeoQA, UniGeo, and Geometry3K.

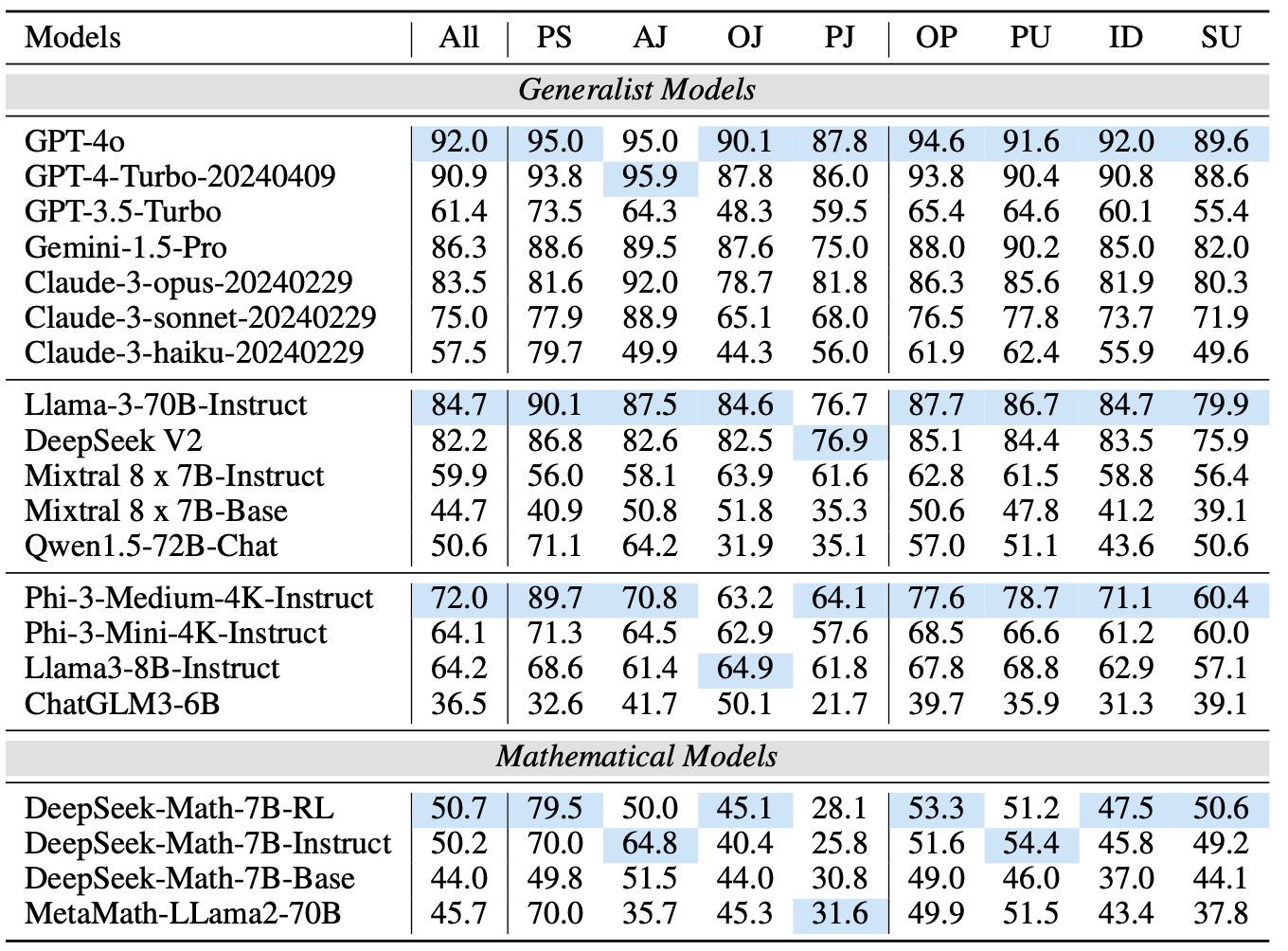
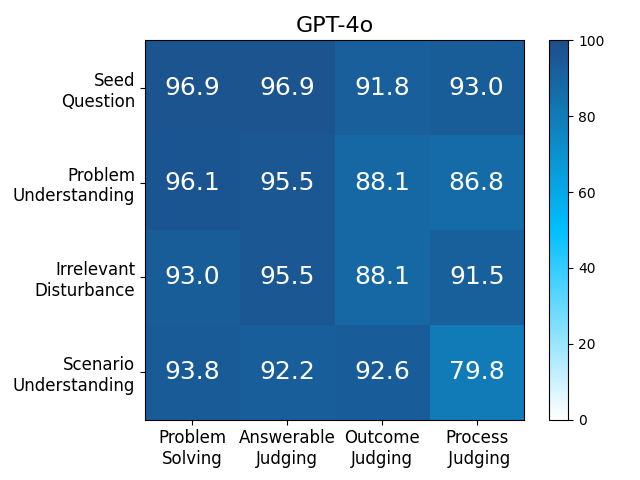
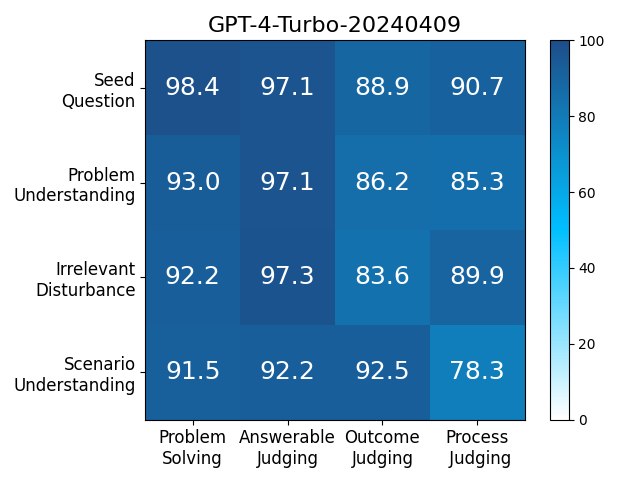
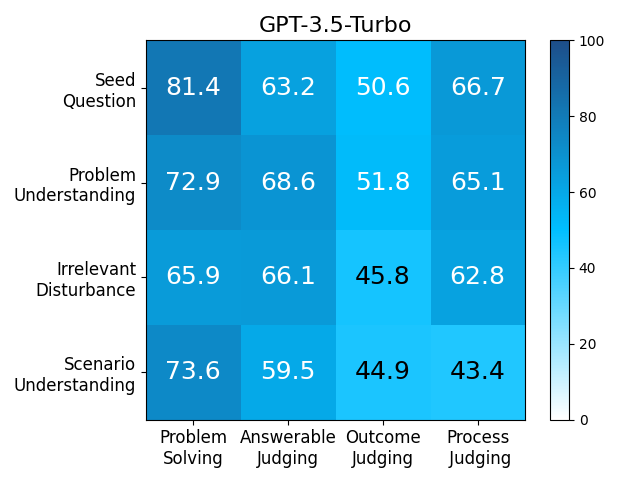
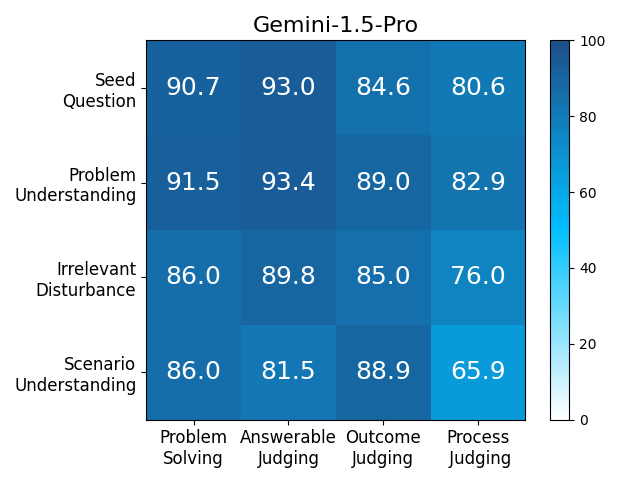
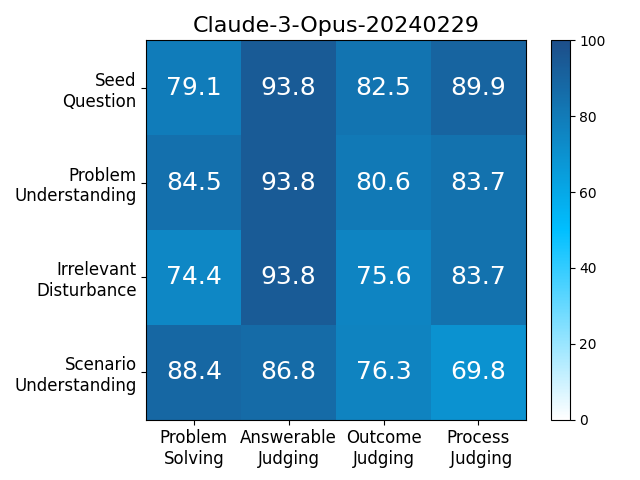
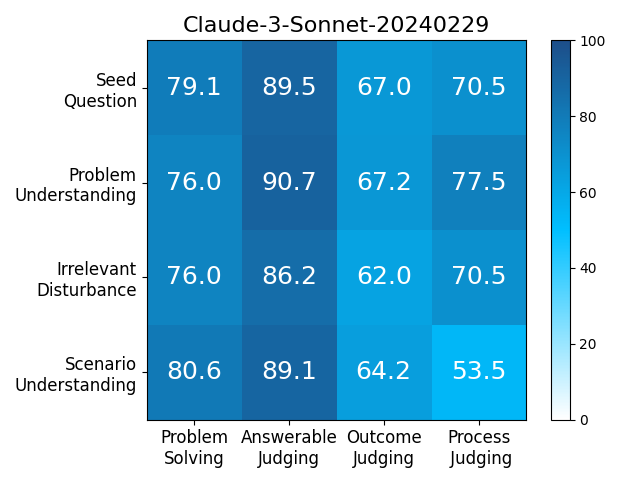
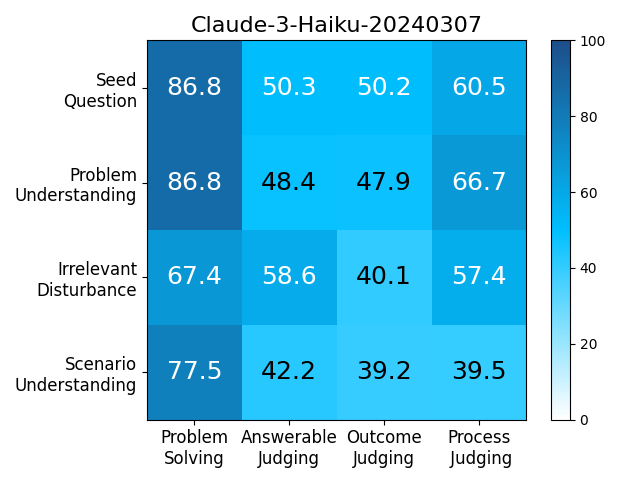
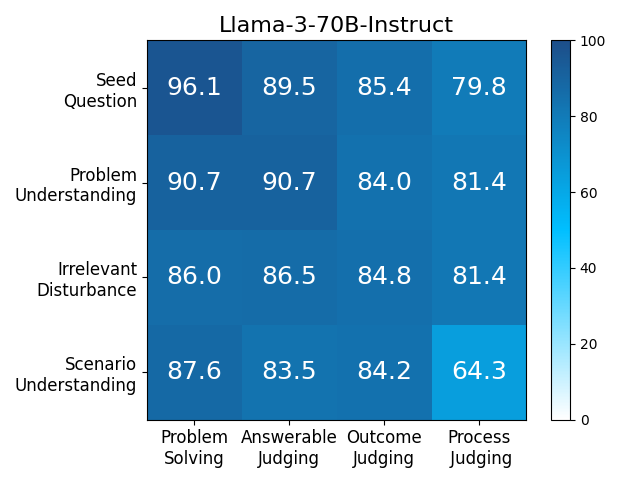
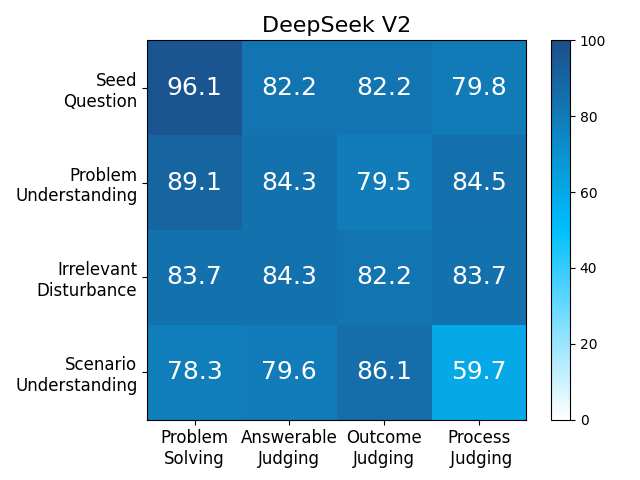
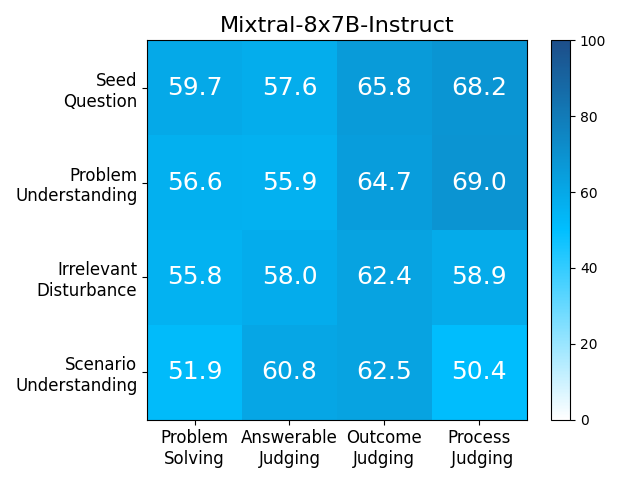
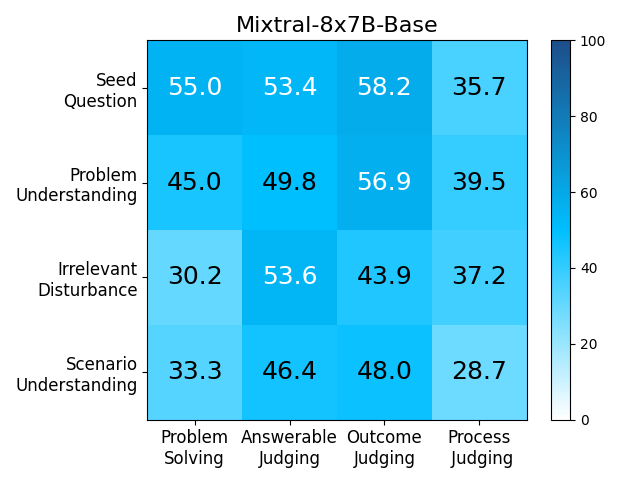
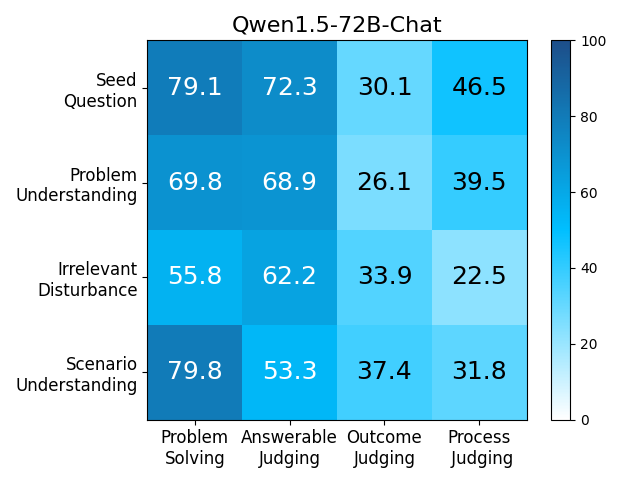
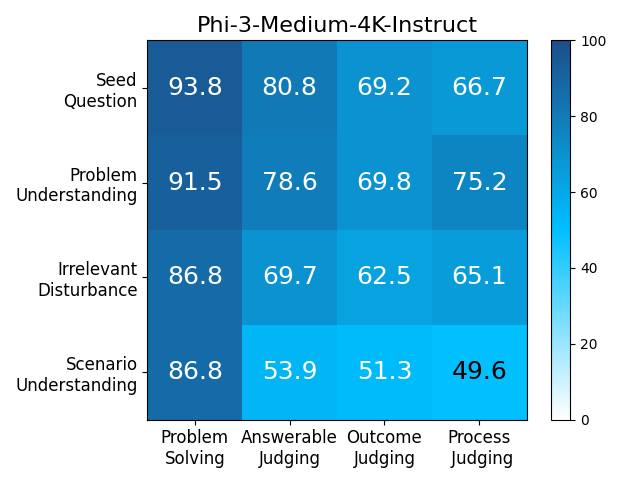
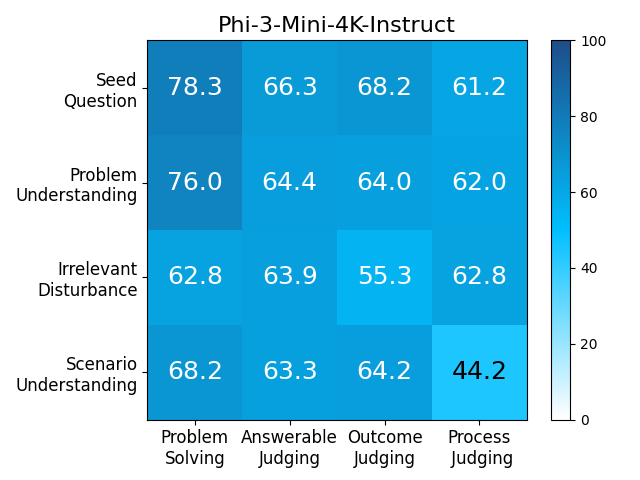
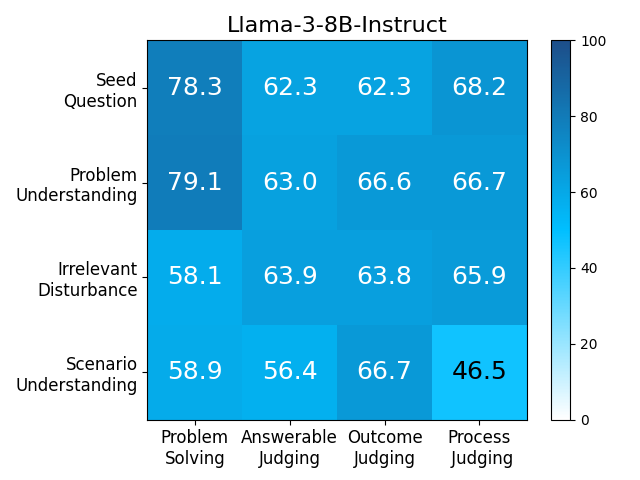
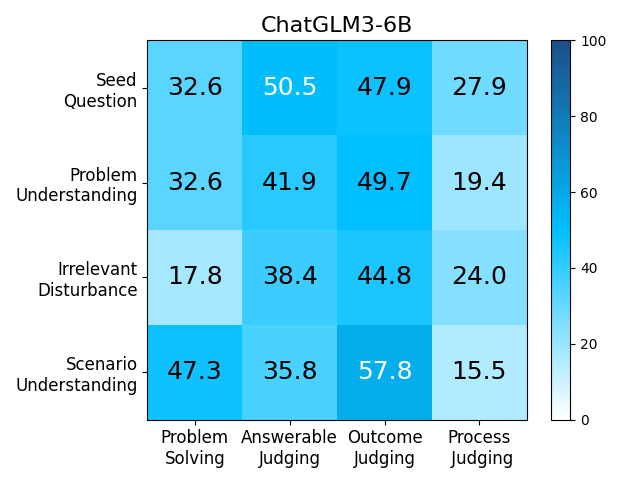
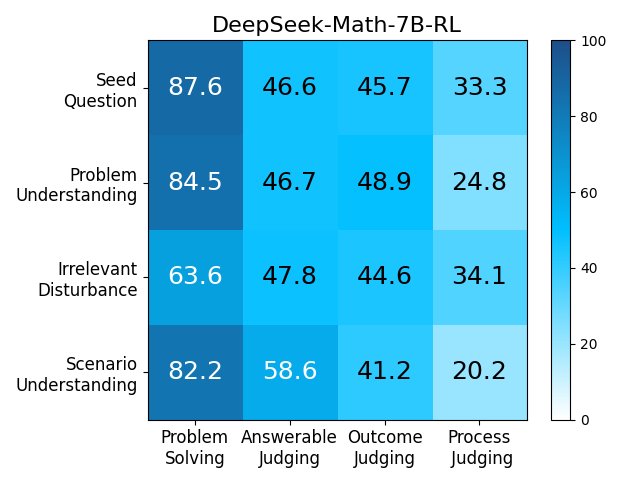
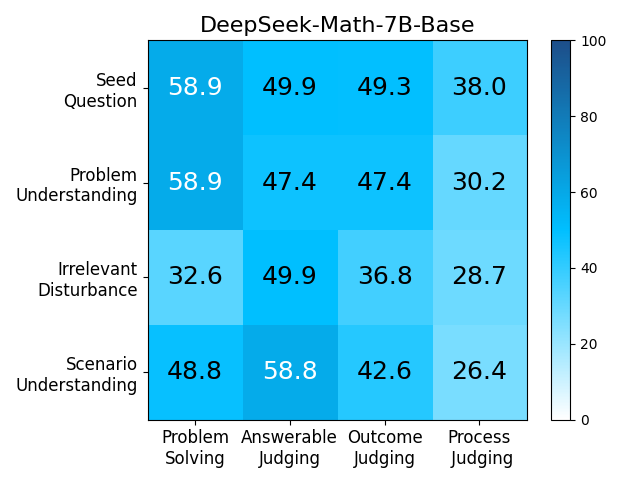
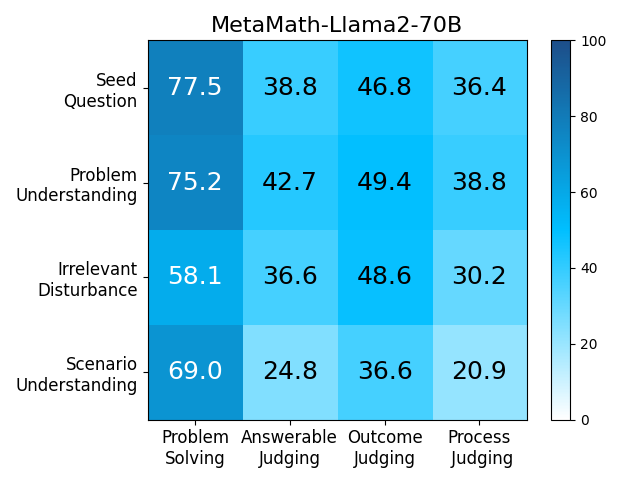
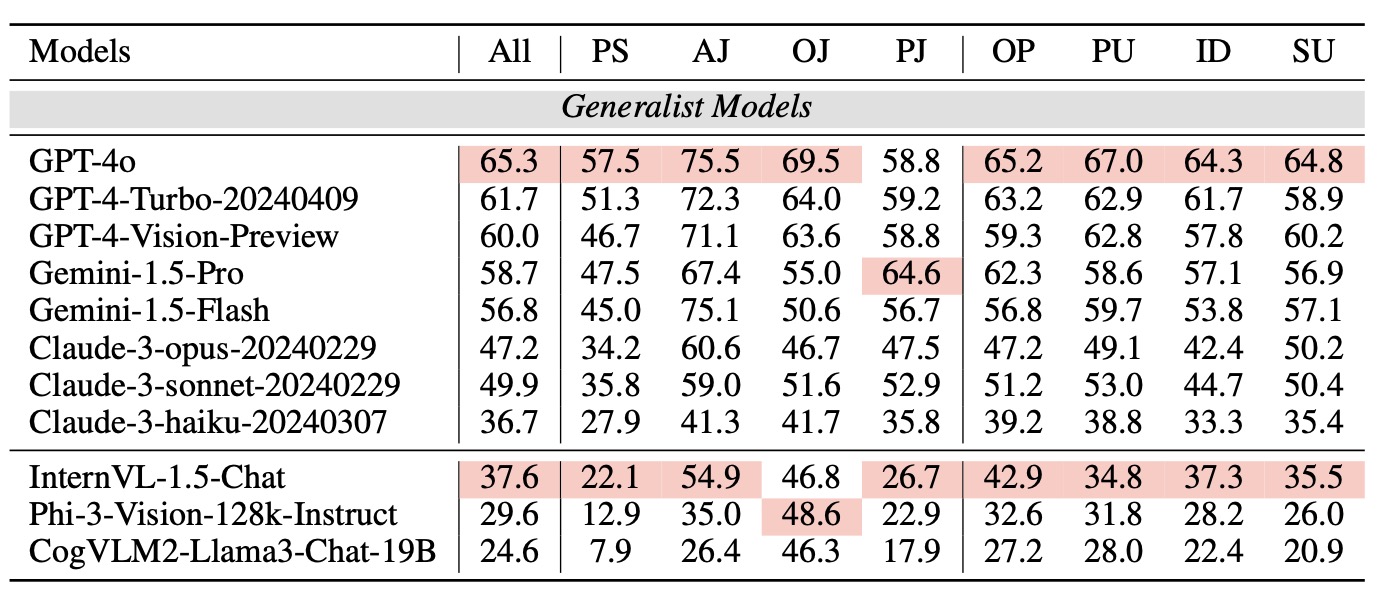
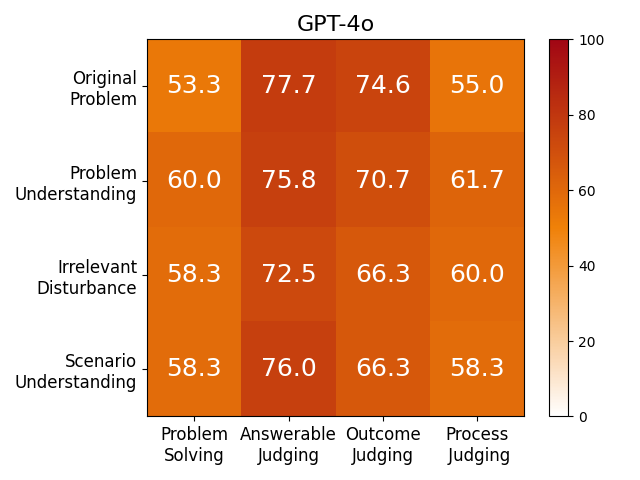
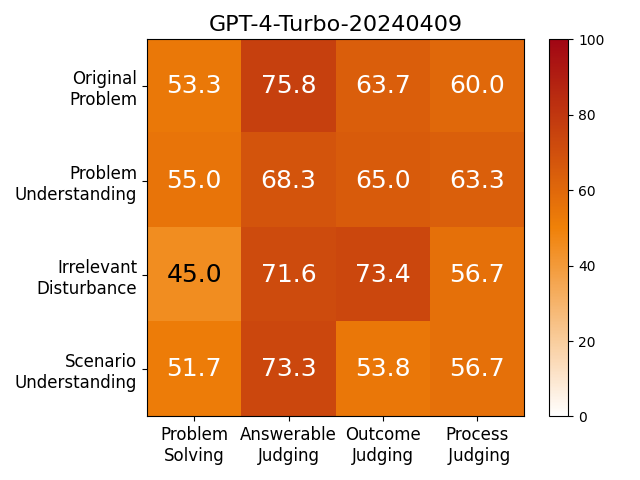
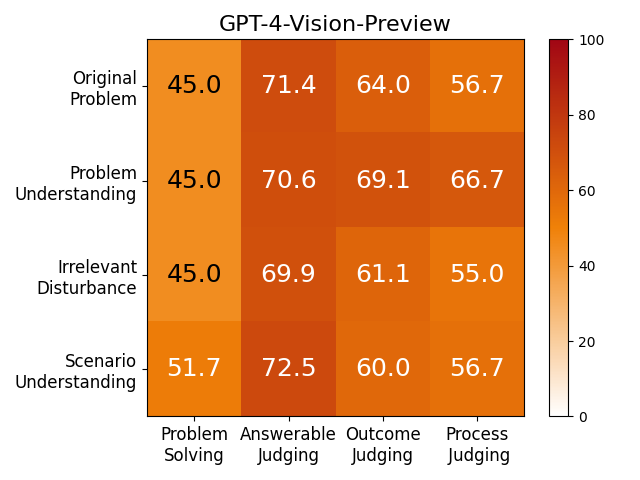
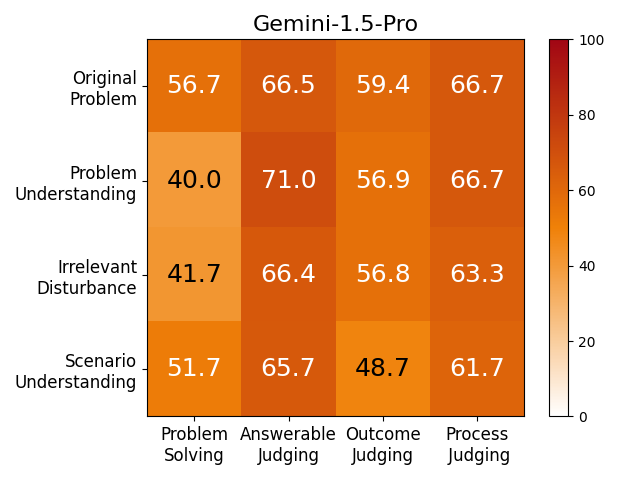
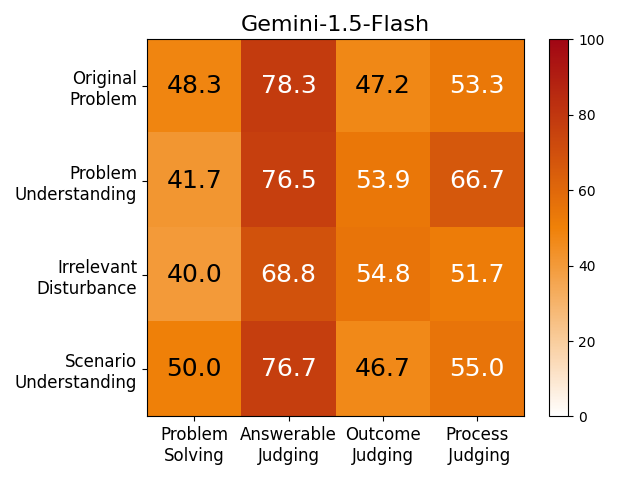
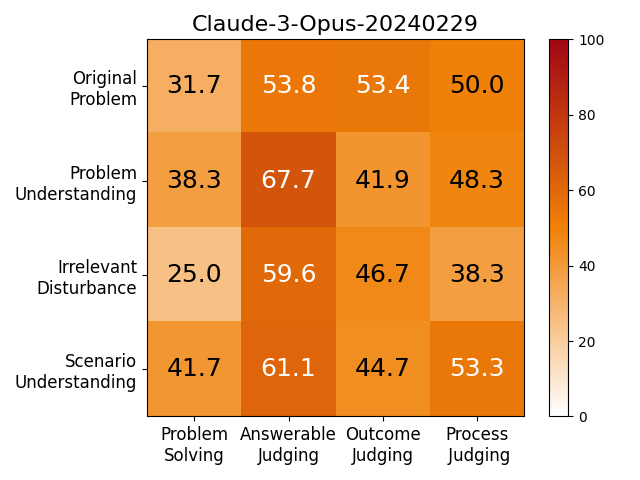
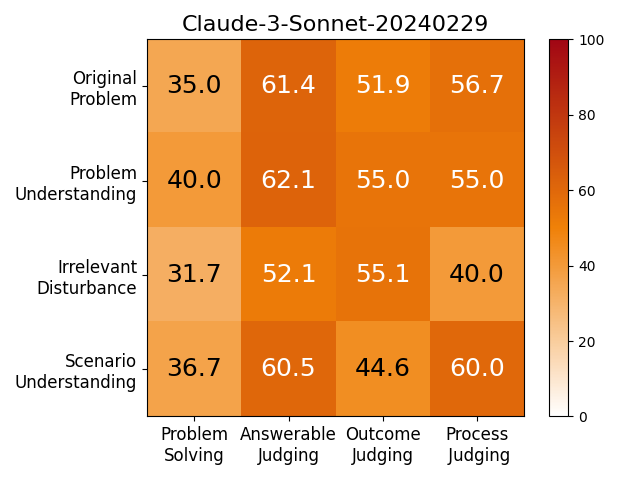
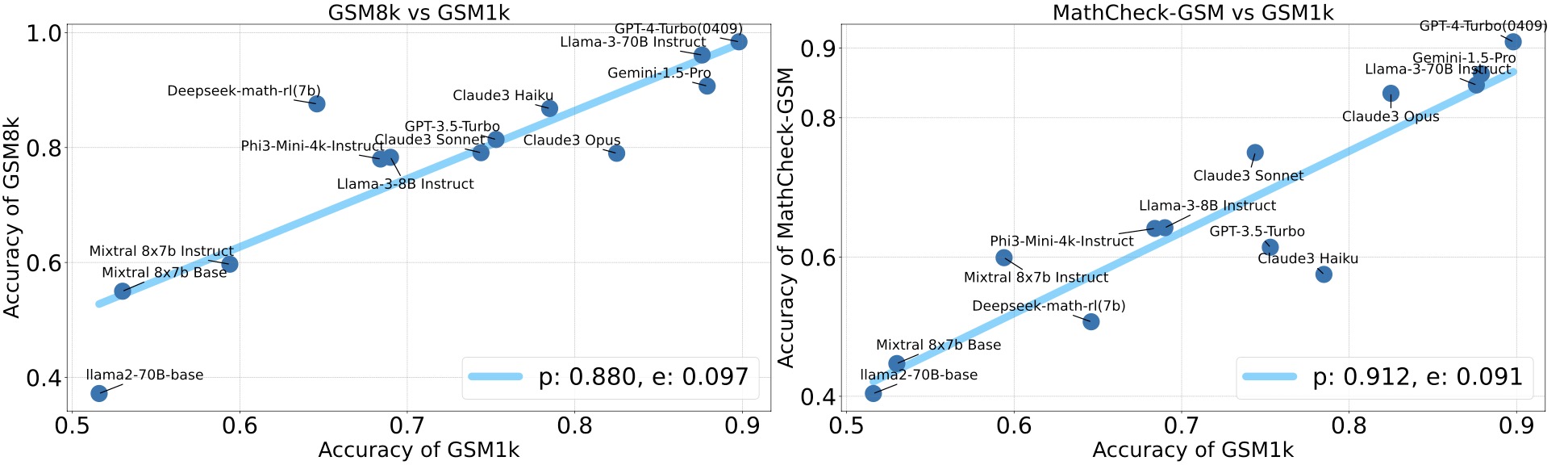
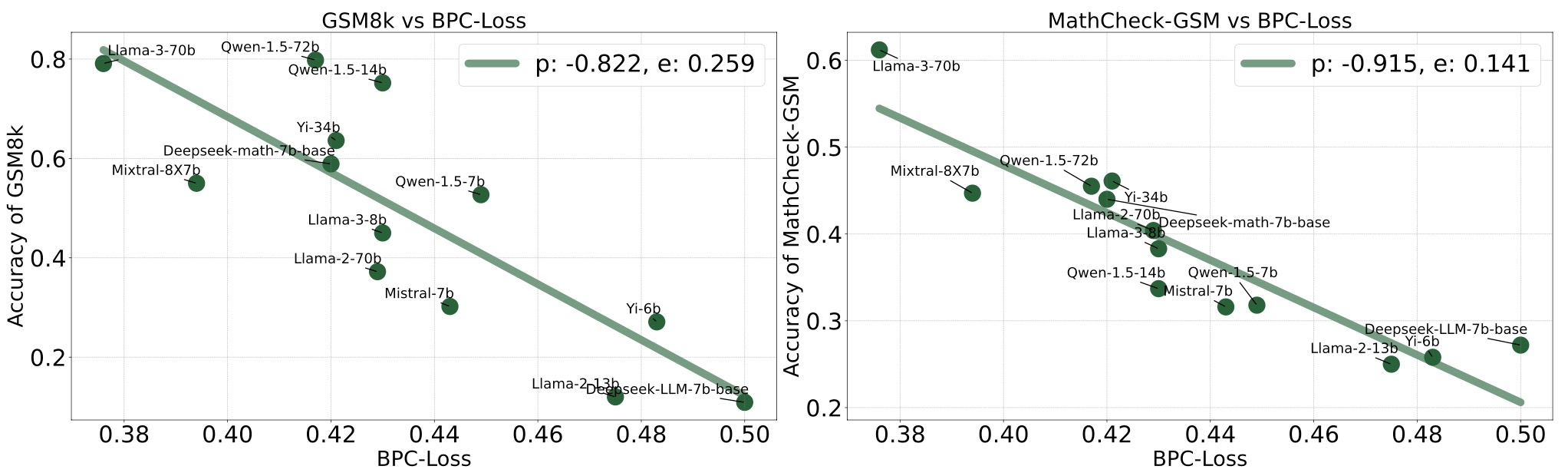
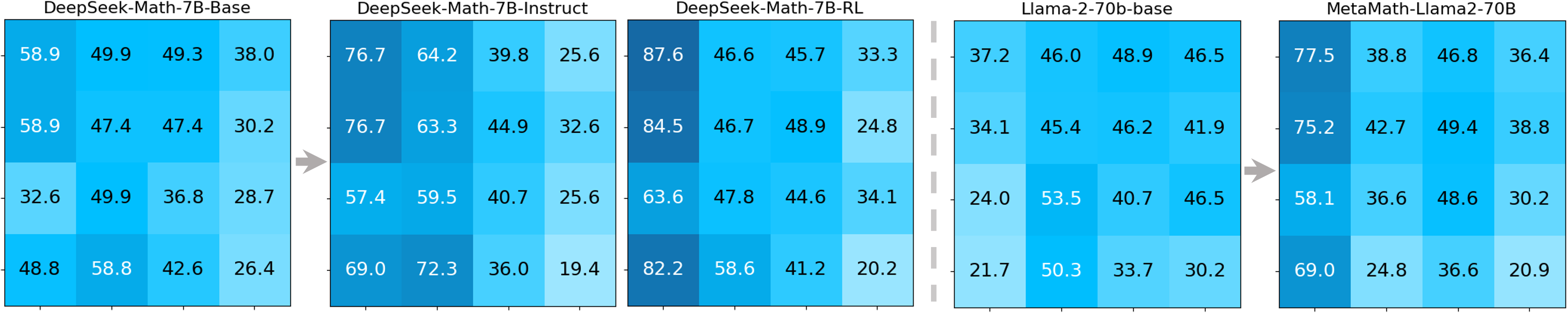
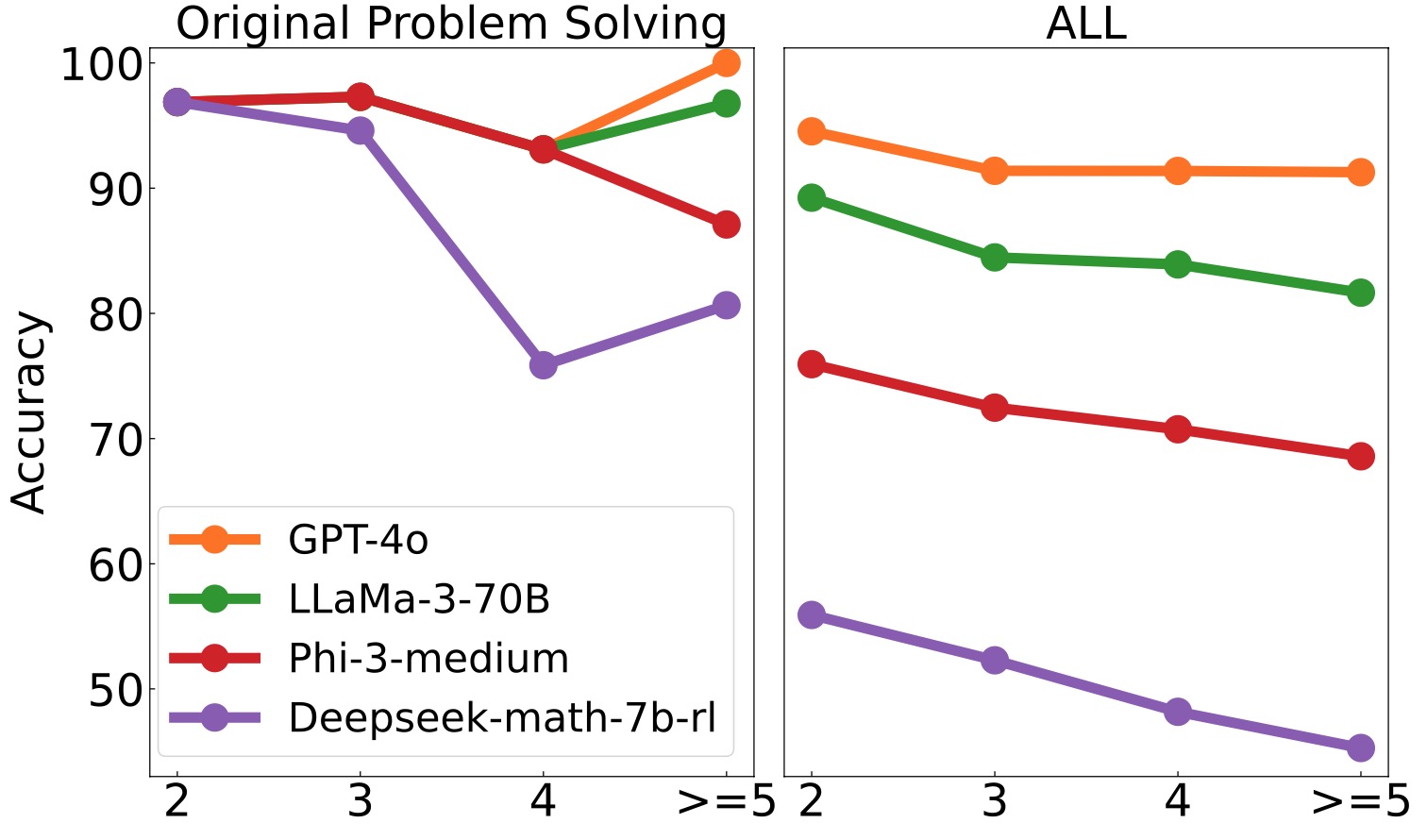
We adopt MATHCHECK-GSM and MATHCHECK-GEO to evaluate over 20 LLMs and 11 MLLMs, assessing their comprehensive mathematical reasoning abilities. Our results demonstrate that while frontier LLMs like GPT-4o continue to excel in various abilities on the checklist, many other model families exhibit a significant decline. Further experiments indicate that, compared to traditional math benchmarks, MATHCHECK better reflects true mathematical abilities and represents mathematical intelligence more linearly, thereby supporting our design. On our MATHCHECK, we can easily conduct detailed behavior analysis to deeply investigate models.

Data Collection

MATHCHECK generation pipeline. We employ (M)LLMs (e.g., GPT-4-Turbo in our experiments) as engines to automatically generate MATHCHECK data. Users first assemble a collection of math problems with labels as seed data. Second, (M)LLMs initially rewrite these problems into their robustness varieties to make up the robustness problem set. Third, each problem in this set will be extended to construct multiple mathematical tasks about this problem.

Experiment Results

LLMs on MATHCHECK-GSM

Model performance on MATHCHECK-GSM. PS: Problem Solving, AJ: Answerable Judging, OJ: Outcome Judging, PJ: Process Judging, OP: Origianl Problem, PU: Problem Understanding, ID: Irrelevant Disturbance, SU: Scenario Understanding. Each score is the average score of related units. For example, All means all units, PS includes solving units on four problem types, OP includes original problems on four tasks units.

LLMs Detailed Results

MLLMs on MATHCHECK-GEO

Model performance on MATHCHECK-GEO.

MLLMs Detailed Results

MATHCHECK-GSM Represents Intelligence More Linearly

Correlation with GSM1k, a dataset that reflects real mathematical reasoning ability. p and e represent the Pearson Correlation Coefficient, and Root Mean Square Error, respectively. By comparing the Pearson correlation coefficient and the root mean square error, it shows that MATHCHECK has a higher correlation coefficient with GSM1k, mitigating bias evaluation caused by overfitting and data contamination.

Performance correlation with BPC-loss, which reflects compression efficiency. The lower BPC-loss represents the higher compression efficiency. Our method shows that many models have scores on our benchmark that align more accurately with their true mathematical abilities.

Behavior Analysis

Behavior of Math Models

Behavior of mathematical models trained on massive solving data. It implies that training solely on massive solving data is not the right direction to improve mathematical reasoning ability. Instead, training models with high-quality and diverse mathematical data, beyond just solving, should be considered.

Reasoning Consistency

In the detailed results above, we can see most of them show good reasoning consistency since they achieve similar scores on each unit, such as GPT series, Llama-3 series and Mixtral series on MATHCHECK-GSM and GPT series on MATHCHECK-GEO. This is an interesting finding as it substantiates our assertion: a model that really understands a problem can robustly work well on multiple related tasks. Meanwhile, we also find that some models perform reasoning inconsistently, show excellent performance on the solving task but much worse in other units of MATHCHECK, These abnormal inconsistency behaviors of generalist models are highly similar to those mathematical models, revealing that they may conduct excessive decoration on original benchmarks.

Behavior on Different Complexity Levels

Performance on different complexity levels (i.e. reasoning steps) of MATHCHECK-GSM. We can observe that the models’ accuracy on the original problem solving fluctuates and does not show an obvious downward trend as the problems are more difficult. While the score “All" shows a steady downward trend, it implies that MATHCHECK better demonstrates the reasoning skills and capabilities required when problems become difficult.

Behavior on Different Prompting Technologies

We evaluate five prompting techniques including Zero-shot, Few-shot, CoT, Least to Most prompting, and Plan-and-Solve prompting on GPT-3.5-turbo. Overall, Chain of Thought (CoT) and Plan-and-Solve (PS) in the zero-shot setting demonstrate superior performance, though this is not consistently the case across all tasks and settings. In contrast, the Few-shot prompt generally yields poorer results than the Zero-shot prompt, particularly in Outcome Judging and Process Judging tasks. Our analysis of the model prediction results indicates that the few-shot setting tends to diminish and abbreviate the reasoning steps. Plan-and-Solve (PS) prompt also does not achieve satisfactory results, potentially due to its problem-decomposition method being less effective for tasks beyond Problem Solving.